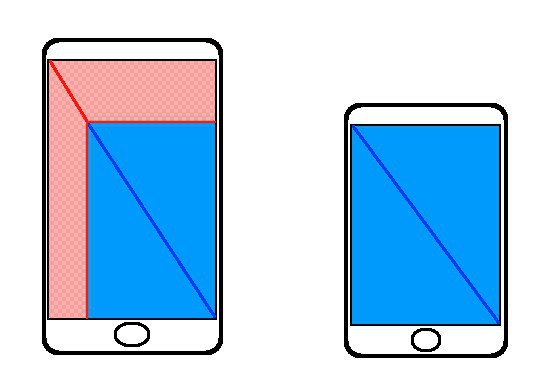
¿Cuál es la diagonal de un cubo y cómo encontrarlo?

¿Qué es un cubo y qué diagonales tiene?

Cubo (poliedro regular o hexaedro)es una forma tridimensional, cada lado es un cuadrado, que, como sabemos, todos los lados son iguales. La diagonal del cubo es el segmento que pasa por el centro de la figura y conecta los vértices simétricos. En un hexaedro regular, hay 4 diagonales, y todas serán iguales. Es muy importante no confundir la diagonal de la figura con la diagonal de su cara o cuadrado, que se encuentra en su base. La diagonal de la cara del cubo pasa por el centro de la cara y conecta los vértices opuestos del cuadrado.

La fórmula por la que puedes encontrar la diagonal del cubo

La diagonal de un poliedro regular se puede encontrarpor una fórmula muy simple para recordar. D = a√3, donde D denota la diagonal del cubo, y a es el borde. Le damos un ejemplo de un problema donde es necesario encontrar una diagonal si se sabe que la longitud de su borde es de 2 cm. Aquí todo es simple D = 2√3, incluso no es necesario contar nada. En el segundo ejemplo, deje que el borde del cubo sea √3 cm, luego obtenemos D = √3√3 = √9 = 3. Respuesta: D es 3 cm.

La fórmula para encontrar la diagonal de la cara del cubo

Diago

La cara también se puede encontrar por la fórmula. Las diagonales que se encuentran en las caras son solo 12 piezas, y todas son iguales. Ahora recuerda d = a√2, donde d es la diagonal del cuadrado, y también es el borde del cubo o el lado del cuadrado. Comprender de dónde vino esta fórmula es muy simple. Después de todo, dos lados de un cuadrado y una diagonal forman un triángulo rectángulo. En este trío, la diagonal desempeña el papel de la hipotenusa, y los lados del cuadrado son las piernas que tienen la misma longitud. Recordemos el teorema de Pitágoras, y todo caerá de inmediato en su lugar. Ahora el problema: el borde del hexaedro es igual a √8 cm, es necesario encontrar la diagonal de su cara. Lo pegamos en la fórmula, y obtenemos d = √8 √2 = √16 = 4. Respuesta: La diagonal de la cara del cubo es de 4 cm.

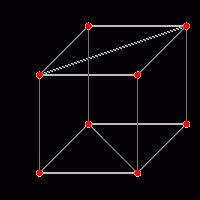
Si se conoce la diagonal de la cara del cubo

Por la condición del problema, se nos da solo la diagonaldel vértice de un poliedro regular, que es, por ejemplo, √2 cm, y tenemos que encontrar la diagonal del cubo. La fórmula para resolver este problema es un poco más complicada que la anterior. Si conocemos d, entonces podemos encontrar el borde del cubo, comenzando desde nuestra segunda fórmula d = a√2. Obtenemos a = d / √2 = √2 / √2 = 1cm (este es nuestro borde). Y si se conoce este valor, entonces encontrar la diagonal del cubo no es difícil: D = 1√3 = √3. Así es como resolvimos nuestro problema.

Si el área de superficie es conocida

El siguiente algoritmo de la solución se basa en encontrar la diagonal sobre el área de la superficie del cubo. Supongamos que es igual a 72 cm². Para empezar, encontramos el área de una cara y todas ellas. Por lo tanto, 72 deben dividirse por 6, obtenemos 12 cm². Esta es el área de una cara. Para encontrar el borde de un poliedro regular, es necesario recordar la fórmula S = a², luego a = √S. Sustituimos y obtenemos a = √12 (el borde del cubo). Y si conocemos este valor, entonces no es difícil encontrar la diagonal D = a√3 = √12 √3 = √36 = 6. Respuesta: la diagonal del cubo es de 6 cm².

Si la longitud de los bordes del cubo es conocida

Hay casos en los que el problema se da solola longitud de todos los bordes del cubo. Entonces es necesario dividir este valor entre 12. Hay tantos lados en el poliedro regular. Por ejemplo, si la suma de todos los bordes es 40, entonces un lado será 40/12 = 3.333. ¡Lo pegamos en nuestra primera fórmula y obtenemos la respuesta!